Zadanie nr 4172048
W kostce mającej kształt sześcianu o krawędzi długości 6 ścięto wszystkie naroża płaszczyznami przechodzącymi przez środki odpowiednich krawędzi (zobacz rysunek). Oblicz objętość otrzymanej bryły.
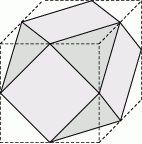
Rozwiązanie
Objętość danej bryły najłatwiej jest obliczyć odejmując od objętości sześcianu objętość odciętych naroży. Na każde naroże możemy patrzeć jak na ostrosłup, który w podstawie ma trójkąt prostokątny o przyprostokątnych długości 3, i który ma wysokość 3. Objętość takiego ostrosłupa jest równa
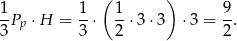
Zatem objętość bryły jest równa
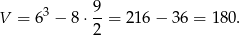
Odpowiedź: 180

