Zadanie nr 4769747
Długość promienia walca zmniejszono dziesięciokrotnie. Ile razy trzeba zwiększyć wysokość tego walca aby objętość się nie zmieniła?
Rozwiązanie
Powiedzmy, że wyjściowy promień podstawy jest równy 
, a wysokość 
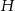. Zatem objętość jest równa
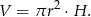
Niech teraz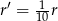 
i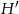 
będą nowymi wymiarami walca, tak aby nie zmieniła się objętość. Mamy równanie
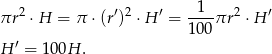
Odpowiedź: Wysokość należy zwiększyć 100 krotnie.
