/Szkoła podstawowa/Geometria/Figury przestrzenne

Zadanie nr 4857042

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego jest równe 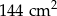14 4 cm 2 . Pole podstawy tej bryły stanowi 80% pola powierzchni bocznej tego ostrosłupa. Oblicz długość krawędzi podstawy tej bryły. Zapisz obliczenia.

Rozwiązanie

Szkicujemy ostrosłup.

PIC

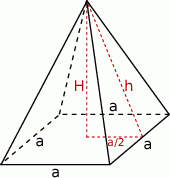
Jeżeli oznaczymy długość krawędzi podstawy przez a , a wysokość ściany bocznej przez 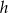h to pole podstawy ostrosłupa jest równe 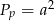Pp = a 2 , a pole powierzchni bocznej jest równe

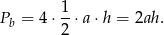
1- Pb = 4 ⋅2 ⋅a ⋅h = 2ah .

Mamy zatem równanie

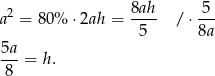
a2 = 8 0% ⋅2ah = 8ah- / ⋅-5- 5 8a 5a ---= h. 8

Wiemy też, że pole powierzchni całkowitej ostrosłupa jest równe 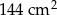144 cm 2 , więc

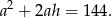
2 a + 2ah = 144.

Podstawiamy w tej równości 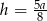5a h = 8 .

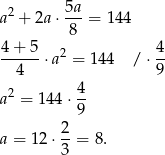
5a a2 + 2a ⋅---= 144 8 4+--5-⋅a2 = 144 / ⋅ 4 4 9 2 4- a = 144 ⋅9 2 a = 12 ⋅--= 8. 3

 
Odpowiedź: 8 cm

Wersja PDF