/Szkoła podstawowa/Geometria/Figury przestrzenne

Zadanie nr 5188710

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole powierzchni bocznej ostrosłupa prawidłowego trójkątnego jest równe 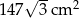√ -- 14 7 3 cm 2 , a pole jego powierzchni całkowitej wynosi 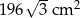√ -- 1 96 3 cm 2 . Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa.

Rozwiązanie

Szkicujemy ostrosłup.

PIC

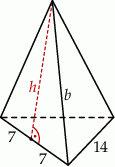
Skoro znamy pole powierzchni bocznej i pole powierzchni całkowitej, to możemy obliczyć pole podstawy.

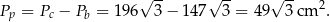
√ -- √ -- √ -- Pp = Pc − Pb = 196 3 − 1 47 3 = 49 3 cm 2.

Za wzoru na pole trójkąta równobocznego mamy więc

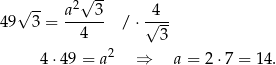
√ -- √ -- a2 3 4 49 3 = ------ /⋅ √--- 4 3 4 ⋅49 = a2 ⇒ a = 2 ⋅7 = 14.

To oznacza, że w podstawie ostrosłupa jest trójkąt równoboczny o boku długości 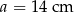a = 14 cm . Jeżeli oznaczmy teraz przez 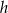h długość wysokości ściany bocznej, to z podanego pola powierzchni bocznej mamy równanie

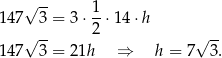
√ -- 1 147 3 = 3 ⋅--⋅14 ⋅h √ -- 2 √ -- 147 3 = 2 1h ⇒ h = 7 3.

Pozostało obliczyć długość 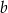b krawędzi bocznej. Korzystamy z twierdzenia Pitagorasa

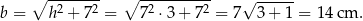
∘ -------- ∘ ---------- b = h2 + 72 = 72 ⋅3+ 72 = 7√ 3-+-1-= 14 cm .

 
Odpowiedź: Krawędź podstawy: 14 cm, krawędź boczna: 14 cm.

Wersja PDF