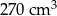Zadanie nr 5601112
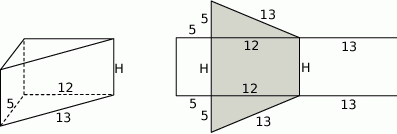
Na rysunku przedstawiono graniastosłup prosty o podstawie trójkąta prostokątnego i jego siatkę. Dwie dłuższe krawędzie podstawy graniastosłupa mają 12 cm i 13 cm długości, a pole zacieniowanej części siatki graniastosłupa jest równe 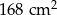 . Oblicz objętość tego graniastosłupa. Zapisz obliczenia.
. Oblicz objętość tego graniastosłupa. Zapisz obliczenia.
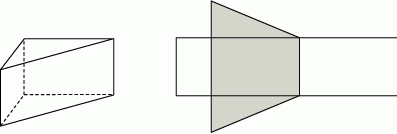
Rozwiązanie
W podstawie graniastosłupa jest trójkąt prostokątny, więc trzecia krawędź podstawy graniastosłupa jest równa
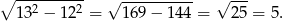
Wysokość 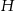 graniastosłupa obliczymy z podanego pola zacieniowanego trapezu. Wysokość tego trapezu to długość dłuższej przyprostokątnej trójkąta w podstawie graniastosłupa, a jego podstawy mają długości
graniastosłupa obliczymy z podanego pola zacieniowanego trapezu. Wysokość tego trapezu to długość dłuższej przyprostokątnej trójkąta w podstawie graniastosłupa, a jego podstawy mają długości 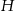 i
i 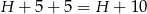 .
.
Mamy zatem
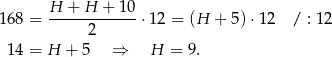
Objętość graniastosłupa jest więc równa
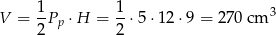
Odpowiedź: