/Szkoła podstawowa/Geometria/Figury przestrzenne

Zadanie nr 6412069

Dodaj do ulubionych
Dodaj do rozwiązanych

Na rysunku przedstawiono dwie różne ściany ostrosłupa prawidłowego czworokątnego. Jedna jest kwadratem o boku 10 cm, a druga – trójkątem równoramiennym o podstawie 10 cm i ramieniu 13 cm.

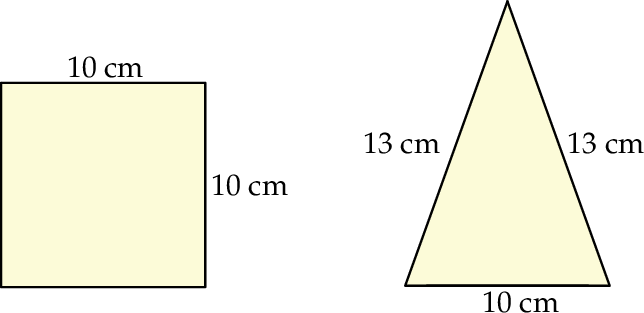
ZINFO-FIGURE

Oblicz pole powierzchni całkowitej ostrosłupa o takich wymiarach.

Rozwiązanie

Dorysujmy wysokość 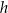h ściany bocznej.

ZINFO-FIGURE

Na mocy twierdzenia Pitagorasa

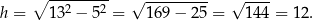
∘ --------- √ --------- √ ---- h = 132 − 52 = 1 69− 25 = 144 = 12.

Pole powierzchni całkowitej ostrosłupa jest więc równe

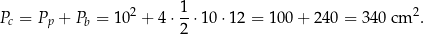
2 1- 2 Pc = Pp + Pb = 10 + 4⋅ 2 ⋅1 0⋅1 2 = 100 + 240 = 340 cm .

 
Odpowiedź: 2 340 cm

Wersja PDF