/Szkoła podstawowa/Geometria/Figury przestrzenne

Zadanie nr 7205341

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego jest równe 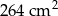26 4 cm 2 . Pole podstawy tej bryły stanowi 75% pola powierzchni jednej ściany bocznej. Oblicz wysokość bryły. Zapisz obliczenia.

Rozwiązanie

Szkicujemy graniastosłup (prostopadłościan).

PIC

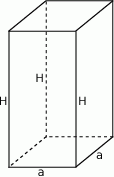
Sposób I

Jeżeli oznaczymy pole podstawy graniastosłupa przez 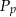Pp , a pole ściany bocznej przez 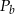Pb to wiemy, że

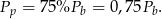
Pp = 7 5%Pb = 0,75Pb .

Korzystamy z informacji o polu powierzchni całkowitej.

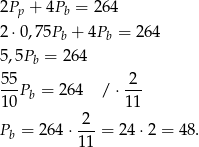
2Pp + 4Pb = 264 2 ⋅0,75Pb + 4Pb = 264 5,5Pb = 264 5 5 2 ---Pb = 2 64 / ⋅--- 1 0 1 1 P = 264 ⋅ 2-= 24⋅2 = 48. b 11

Stąd

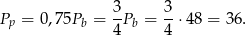
Pp = 0,75Pb = 3Pb = 3⋅ 48 = 36. 4 4

Podstawa graniastosłupa jest więc kwadratem o boku 6 cm. To pozwala obliczyć długość wysokości 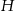H .

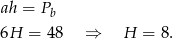
ah = Pb 6H = 4 8 ⇒ H = 8.

Sposób II

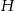Oznaczmy przez a długość podstawy graniastosłupa, a przez H długość jego wysokości. Z informacji o stosunku pól podstawy i ściany bocznej mamy

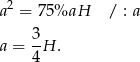
a2 = 75%aH / : a a = 3H . 4

Korzystamy teraz z informacji o polu całkowitym

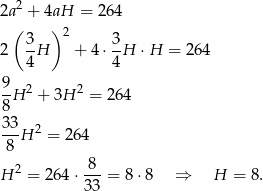
2 2a + 4aH = 2 64 ( 3 ) 2 3 2 --H + 4 ⋅--H ⋅H = 2 64 4 4 9- 2 2 8 H + 3H = 264 33 ---H 2 = 264 8 H 2 = 264 ⋅-8-= 8 ⋅8 ⇒ H = 8. 33

 
Odpowiedź: 8 cm

Wersja PDF