Zadanie nr 8253150
Z 36 identycznych plastikowych sześcianów o krawędzi długości 1 cm zbudowano graniastosłup prawidłowy czworokątny. Jakie jest największe możliwe pole powierzchni tego graniastosłupa? Zapisz obliczenia.
Rozwiązanie
Zastanówmy się, jakie mogą być wymiary utworzonego graniastosłupa.
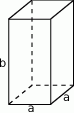
Ponieważ graniastosłup ma być prawidłowy, dwie jego krawędzie muszą mieć tę samą długość. Ponadto, iloczyn długości krawędzi musi być równy 36 (bo tyle musi być równa objętość graniastosłupa). Szukamy zatem wszystkich możliwych rozkładów postaci:
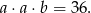
Są cztery możliwości:
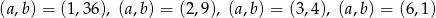
Zauważmy, że pole powierzchni graniastosłupa jest równe
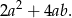
Pola powierzchni możliwych graniastosłupów są więc kolejno równe
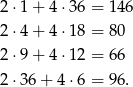
Największe pole powierzchni otrzymujemy więc w przypadku graniastosłupa o wymiarach
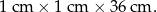
Odpowiedź: