/Szkoła podstawowa/Geometria/Figury przestrzenne

Zadanie nr 9970012

Dodaj do ulubionych
Dodaj do rozwiązanych

W graniastosłupie prawidłowym sześciokątnym wszystkie krawędzie mają jednakową długość. Oblicz objętość tego graniastosłupa jeżeli jego pole powierzchni całkowitej jest równe 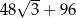√ -- 48 3+ 96 .

Rozwiązanie

Zaczynamy od rysunku i oznaczmy długość krawędzi graniastosłupa przez a .

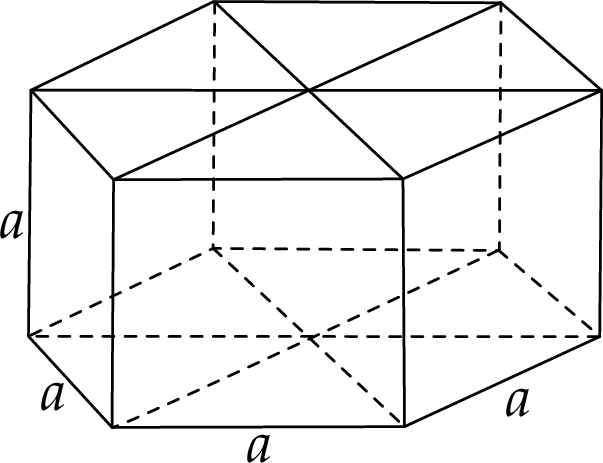
ZINFO-FIGURE

Sześciokąt foremny w podstawie graniastosłupa składa się z 6 trójkątów równobocznych o boku a , więc pole powierzchni całkowitej graniastosłupa jest równe

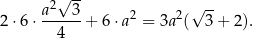
-- a2√ 3 √ -- 2⋅6 ⋅------+ 6⋅a2 = 3a2( 3+ 2). 4

Z podanego pola powierzchni całkowitej mamy więc równanie

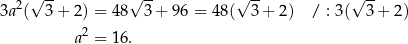
2 √ -- √ -- √ -- √ -- 3a ( 3 + 2) = 48 3+ 9 6 = 48( 3 + 2) / : 3( 3 + 2) a2 = 16 .

Zatem 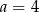a = 4 i objętość graniastosłupa jest równa

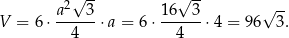
√ -- √ -- a2--3- 16---3 √ -- V = 6 ⋅ 4 ⋅a = 6 ⋅ 4 ⋅ 4 = 96 3.

 
Odpowiedź: √ -- V = 96 3

Wersja PDF