Zadanie nr 2057082
Wartość wyrażenia 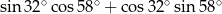 jest równa
jest równa
A) 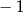 B) 1 C) 0 D) 2
B) 1 C) 0 D) 2
Rozwiązanie
Sposób I
Skorzystamy z następujących wzorów
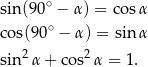
Liczymy
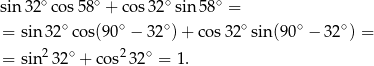
Sposób II
Tym razem skorzystamy ze wzoru na sinus sumy.
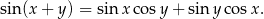
Liczymy
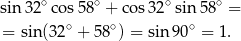
Odpowiedź: B
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wartość wyrażenia 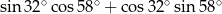 jest równa
jest równa
A) 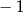 B) 1 C) 0 D) 2
B) 1 C) 0 D) 2
Sposób I
Skorzystamy z następujących wzorów
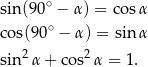
Liczymy
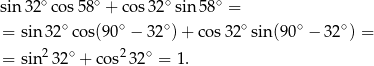
Sposób II
Tym razem skorzystamy ze wzoru na sinus sumy.
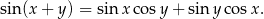
Liczymy
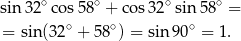
Odpowiedź: B
