/Szkoła średnia/Zadania testowe/Funkcje/Trygonometryczna/Wartość wyrażenia/Bez ułamka

Zadanie nr 2156140

Dodaj do ulubionych
Dodaj do rozwiązanych

Wartość wyrażenia 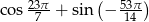23π- ( 53π) cos 7 + sin − 14 jest równa
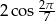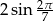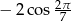
A) 0 B) 2 cos 2π7-- C) 2 sin 2π- 7 D) − 2 cos 2π 7

Rozwiązanie

Sprowadzamy najpierw kąty do przedziału 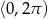⟨0,2π ) – w tym celu odejmujemy lub dodajemy wielokrotności 2π .

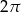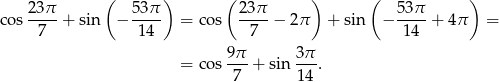
( ) ( ) ( ) cos 23π-+ sin − 53π- = cos 23π-− 2 π + sin − 53π- + 4π = 7 14 7 14 9π 3π = cos ---+ sin ---. 7 1 4

Chcemy oba te kąty sprowadzić do kąta 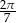2π7- , więc korzystamy teraz ze wzorów redukcyjnych

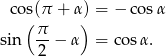
cos(π + α) = − co sα ( π- ) sin 2 − α = cos α.

Mamy zatem

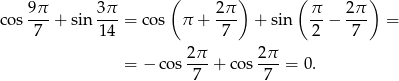
( ) ( ) 9-π 3π- 2π- π- 2π- cos 7 + sin 14 = cos π + 7 + sin 2 − 7 = = − co s 2π + cos 2π- = 0. 7 7

 
Odpowiedź: A

Wersja PDF