Zadanie nr 9340053
Kąt ostry  jest większy od kąta ostrego
jest większy od kąta ostrego 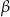 . Wynika stąd, że
. Wynika stąd, że
A) 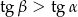 B)
B) 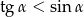 C)
C) 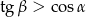 D)
D) 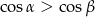
Rozwiązanie
Zaczynamy od rysunku
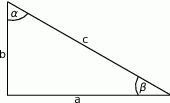
Wypiszmy wartość interesujących nas funkcji trygonometrycznych
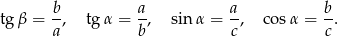
Dla kątów ostrych funkcja tangens jest rosnąca, więc
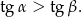
Ponieważ 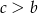 , więc
, więc 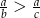 . Zatem
. Zatem
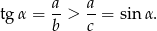
Ponieważ 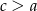 , więc
, więc 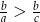 . Zatem
. Zatem
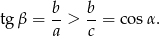
Funkcja cosinus jest malejąca dla kątów ostrych oraz 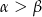 , więc
, więc
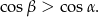
Odpowiedź: C

