/Szkoła średnia/Zadania testowe/Funkcje/Wielomiany/Dwa wielomiany/Iloczyn

Zadanie nr 4510924

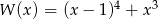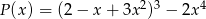Iloczyn wielomianów 4 3 W (x) = (x − 1) + x i 2 3 4 P (x) = (2 − x + 3x ) − 2x jest wielomianem stopnia
A) 24 B) 10 C) 12 D) 7

Wersja PDF

Rozwiązanie

Zauważmy, że wymnażając nawiasy

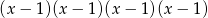
(x− 1)(x− 1)(x − 1)(x − 1)

otrzymamy wielomian stopnia 4, czyli 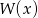W (x ) jest wielomianem stopnia 4.

Podobnie, wyrażenie

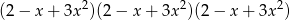
(2 − x + 3x2)(2 − x + 3x 2)(2− x+ 3x2)

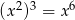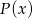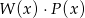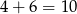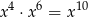jest wielomianem z najwyższą potęgą x postaci: (x2)3 = x6 , czyli P(x ) jest wielomianem stopnia 6. Zatem iloczyn W (x )⋅P (x) będzie wielomianem stopnia 4 + 6 = 10 (bo 4 6 10 x ⋅x = x ).  
Odpowiedź: B

Wersja PDF