/Szkoła średnia/Zadania testowe/Funkcje/Wielomiany/Dwa wielomiany/Iloczyn

Zadanie nr 9194108

Dane są dwa wielomiany 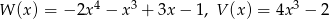4 3 3 W (x) = − 2x − x + 3x − 1 , V (x) = 4x − 2 . Stopień wielomianu 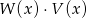W (x )⋅V (x) jest równy
A) 12 B) 7 C) 4 D) 3

Wersja PDF

Rozwiązanie

Sposób I

Mnożymy podane wielomiany

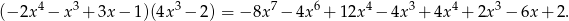
4 3 3 7 6 4 3 4 3 (− 2x − x + 3x − 1)(4x − 2) = − 8x − 4x + 12x − 4x + 4x + 2x − 6x + 2.

Widać, że stopień otrzymanego wielomianu jest równy 7.

Sposób II

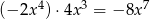Tak naprawdę nie musimy wykonywać całego mnożenia, wystarczy przemnożyć przez siebie najwyższe potęgi x z obu wielomianów. Widać, że da nam to: (− 2x 4) ⋅4x3 = − 8x7 i to będzie najwyższa potęga x w wyniku. Tego typu rachunek można swobodnie przeprowadzić w pamięci.  
Odpowiedź: B

Wersja PDF