/Szkoła podstawowa/Geometria/Figury przestrzenne/Graniastosłupy

Zadanie nr 4763853

Pole powierzchni bocznej graniastosłupa prawidłowego sześciokątnego jest równe 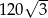√ -- 12 0 3 , a pole jego powierzchni całkowitej wynosi 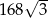√ -- 168 3 . Oblicz długość krawędzi podstawy i długość przekątnej ściany bocznej tego graniastosłupa. Zapisz obliczenia.

Wersja PDF

Rozwiązanie

Szkicujemy graniastosłup.

PIC

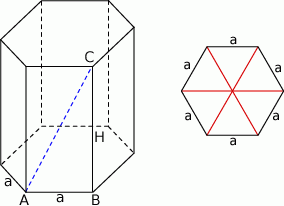
Skoro znamy pole powierzchni bocznej 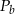Pb i pole powierzchni całkowitej 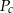Pc , to możemy obliczyć pole podstawy Pp .

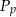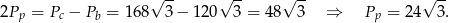
√ -- √ -- √ -- √ -- 2Pp = Pc − Pb = 16 8 3− 120 3 = 4 8 3 ⇒ Pp = 24 3.

Podstawą graniastosłupa jest sześciokąt foremny – jest to figura składająca się z 6 trójkątów równobocznych, więc jeżeli przez a oznaczymy długość jego boku, to korzystając ze wzoru na pole trójkąta równobocznego mamy

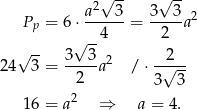
√ -- √ -- a2 3 3 3 Pp = 6 ⋅------= ----a 2 √ --4 2 √ -- 3--3- 2 --2-- 2 4 3 = 2 a / ⋅3 √ 3- 2 16 = a ⇒ a = 4.

Obliczmy teraz z podanego pola powierzchni bocznej długość wysokości graniastosłupa.

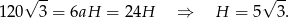
√ -- √ -- 120 3 = 6aH = 24H ⇒ H = 5 3.

Długość przekątnej ściany bocznej obliczamy z trójkąta prostokątnego 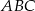ABC .

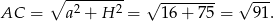
∘ -2-----2 √ -------- √ --- AC = a + H = 16 + 75 = 91.

 
Odpowiedź: Krawędź podstawy: 4, przekątna ściany bocznej: 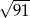√ --- 91 .

Wersja PDF