/Szkoła podstawowa/Geometria/Figury przestrzenne/Graniastosłupy

Zadanie nr 7756810

Oskar zrobił dwa pudełka w kształcie graniastosłupów prawidłowych: czworokątnego i sześciokątnego. Powierzchnię boczną każdego z tych graniastosłupów wykonał z takich samych prostokątów o wymiarach 24 cm i 12 cm (patrz rysunek). Oblicz stosunek objętości tych graniastosłupów oraz ustal, który z nich ma większą objętość.

PIC

Wersja PDF

Rozwiązanie

Podstawą pierwszego graniastosłupa jest kwadrat o boku 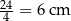24 4 = 6 cm , więc jego objętość jest równa

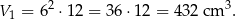
V1 = 62 ⋅12 = 3 6⋅12 = 432 cm 3.

Podstawą drugiego graniastosłupa jest sześciokąt foremny o boku 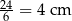246 = 4 cm .

PIC

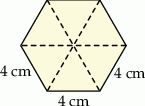
Jego objętość jest równa

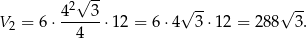
2√ -- V = 6 ⋅ 4--3-⋅1 2 = 6⋅ 4√ 3⋅ 12 = 288√ 3-. 2 4

Stosunek objętości jest więc równy

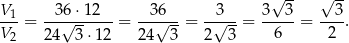
√ -- √ -- V1- --3√6⋅-12-- --3√6-- -√3-- 3--3- --3- V2 = 24 3 ⋅12 = 24 3 = 2 3 = 6 = 2 .

W szczególności

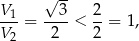
√ -- V1 3 2 ---= ----< --= 1, V2 2 2

więc drugi z graniastosłupów ma większą objętość.  
Odpowiedź: 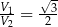√ - VV1= -23 2 , V2 > V1

Wersja PDF