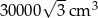/Szkoła podstawowa/Geometria/Figury przestrzenne/Graniastosłupy

Zadanie nr 9178939

Dodaj do ulubionych
Dodaj do rozwiązanych

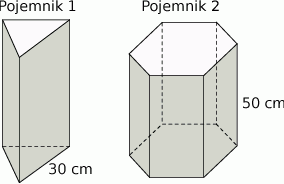
Dwa pojemniki mają kształt graniastosłupów prawidłowych, przy czym pierwszy ma kształt graniastosłupa trójkątnego o krawędzi podstawy długości 30 cm, a drugi sześciokątnego o wysokości 50 cm. Objętość pierwszego pojemnika stanowi 45% objętości drugiego pojemnika i jest mniejsza od tej objętości o 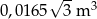√ -- 3 0,01 65 3 m . Oblicz objętości obu pojemników.

PIC

Rozwiązanie

Zauważmy najpierw, że

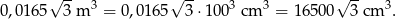
√ -- 3 √ -- 3 3 √ -- 3 0,0165 3 m = 0 ,0165 3 ⋅100 cm = 1650 0 3 cm .

Sposób I

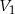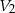Jeżeli oznaczymy przez V 1 i V 2 objętości odpowiednio pierwszego i drugiego graniastosłupa, to

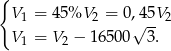
{ V1 = 4 5%V 2 = 0,√45V 2 V1 = V 2 − 16500 3.

Podstawiamy teraz 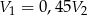V = 0 ,45V 1 2 z pierwszego równania do drugiego

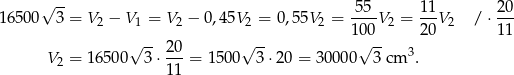
√ -- 5-5- 11- 20- 16500 3 = V2 − V1 = V2 − 0,45V 2 = 0,55V2 = 100V 2 = 20 V2 / ⋅ 11 √ -- 20 √ -- √ -- V 2 = 16500 3⋅ ---= 15 00 3⋅ 20 = 3000 0 3 cm 3. 11

Stąd

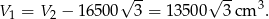
√ -- √ -- 3 V1 = V 2 − 16 500 3 = 13 500 3 cm .

Sposób II

Jeżeli oznaczymy przez 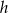h wysokość pierwszego graniastosłupa, a przez a krawędź podstawy drugiego graniastosłupa, to ich objętości są odpowiednio równe

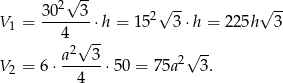
2√ -- √ -- √ -- V = 3-0---3 ⋅h = 152 3 ⋅h = 2 25h 3 1 4 √ -- a2 3 √ -- V2 = 6 ⋅------⋅50 = 75a2 3. 4

Podane informacje o objętościach graniastosłupów prowadzą więc do układu równań

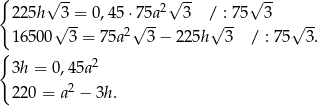
{ √ -- 2√ -- √ -- 225h √3 = 0,45 ⋅√75a 3 /√ : 75 3 √ -- 16500 3 = 75a2 3 − 22 5h 3 / : 75 3. { 3h = 0 ,45a2 2 220 = a − 3h .

Podstawiamy 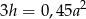2 3h = 0,45a z pierwszego równania do drugiego

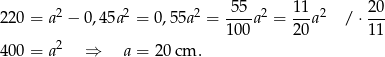
55 11 20 220 = a2 − 0,45a 2 = 0,55a2 = ---a2 = --a2 /⋅ --- 100 20 11 400 = a2 ⇒ a = 20 cm .

Stąd

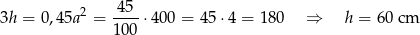
3h = 0,45a2 = 45--⋅400 = 45⋅4 = 180 ⇒ h = 60 cm 100

i objętości graniastosłupów są równe

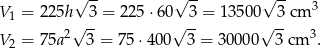
√ -- √ -- √ -- 3 V1 = 225h 3 = 225⋅ 60 3 = 13 500 3 cm 2√ -- √ -- √ -- 3 V2 = 75a 3 = 75 ⋅400 3 = 30000 3 cm .

 
Odpowiedź: 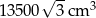√ -- 135 00 3 cm 3 i √ -- 30000 3 cm 3

Wersja PDF