Zadanie nr 1930697
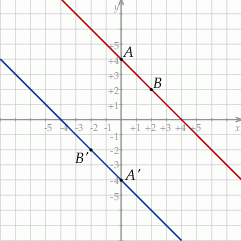
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 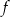 . Na wykresie tej funkcji leżą punkty
. Na wykresie tej funkcji leżą punkty 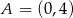 i
i 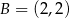 .
.
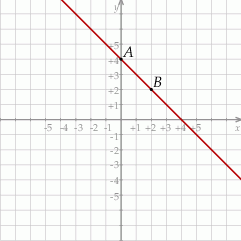
Obrazem prostej 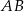 w symetrii względem początku układu współrzędnych jest wykres funkcji
w symetrii względem początku układu współrzędnych jest wykres funkcji 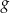 określonej wzorem
określonej wzorem
A) 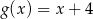 B)
B) 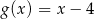 C)
C) 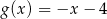 D)
D) 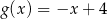
Rozwiązanie
Sposób I
Jeżeli odbijemy dany wykres funkcji liniowej względem początku układu współrzędnych, to otrzymamy prostą przechodzącą przez punkty 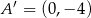 i
i 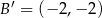 .
.
Jest to więc prosta postaci 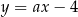 . Współczynnik
. Współczynnik  wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 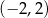 .
.

Odbita prosta ma więc równanie 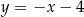 .
.
Sposób II
Dana prosta przechodzi przez punkt 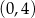 , więc ma równanie postaci
, więc ma równanie postaci 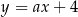 . Przechodzi ponadto przez punkt
. Przechodzi ponadto przez punkt 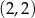 , więc
, więc
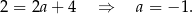
Jest to więc prosta 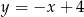 . Prosta symetryczna do niej względem początku układu współrzędnych ma ten sam współczynnik kierunkowy, bo tworzy z osią
. Prosta symetryczna do niej względem początku układu współrzędnych ma ten sam współczynnik kierunkowy, bo tworzy z osią 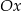 taki sam kąt jak pierwsza prosta. Ponadto przecina oś
taki sam kąt jak pierwsza prosta. Ponadto przecina oś 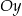 w punkcie
w punkcie 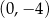 , więc jest to prosta:
, więc jest to prosta: 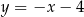 .
.
Odpowiedź: C

