/Szkoła średnia/Zadania testowe/Funkcje - wykresy/Parabola/Punkty wspólne z osiami

Zadanie nr 4320063

Wskaż wzór funkcji, która przecina osie układu współrzędnych w 3 punktach.
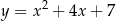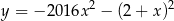
A) y = x 2 + 4x + 7 B) y = − 201 6x2 − (2+ x)2
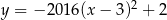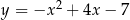
C) 2 y = − 201 6(x− 3) + 2 D) 2 y = −x + 4x − 7

Wersja PDF

Rozwiązanie

Wykres każdej funkcji kwadratowej przecina oś 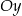Oy w dokładnie jednym punkcie (aby go znaleźć wystarczy obliczyć 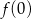f(0 ) ). Pytanie zatem brzmi: która z podanych funkcji ma dwa miejsca zerowe.

Jeżeli ktoś ma dobre oczy, to powinien szybko spostrzec, że wykresem funkcji

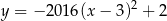
2 y = − 2016(x − 3 ) + 2

jest parabola o ramionach skierowanych w dół i wierzchołku powyżej osi 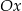Ox . Ma więc ona dwa pierwiastki.

Jeżeli jednak nie zauważyliśmy tego od razu, to sprawdzamy pozostałe funkcje. Łatwo sprawdzić, że trójmiany

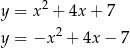
y = x2 + 4x+ 7 2 y = −x + 4x − 7

mają ujemną 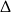Δ -ę, więc nie mają pierwiastków. Ponadto wyrażenie 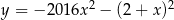y = − 2016x2 − (2 + x)2 jest stale ujemne, więc nie może mieć pierwiastków.  
Odpowiedź: C

Wersja PDF