/Szkoła średnia/Zadania testowe/Funkcje - wykresy/Parabola/Punkty wspólne z osiami

Zadanie nr 5787273

Punkty 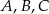A ,B,C są punktami przecięcia paraboli o równaniu 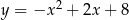2 y = −x + 2x + 8 z osiami układu współrzędnych. Pole trójkąta 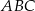ABC jest równe
A) 8 B) 9 C) 24 D) 27

Wersja PDF

Rozwiązanie

Dany wykres przecina oś 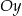Oy w punkcie

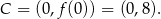
C = (0,f(0)) = (0,8 ).

Aby wyznaczyć punkty przecięcia z osią 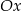Ox rozwiązujemy równanie

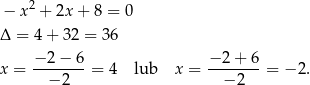
2 − x + 2x + 8 = 0 Δ = 4 + 32 = 36 x = −-2-−-6 = 4 lub x = −-2-+-6 = − 2. − 2 − 2

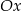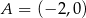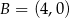Wykres przecina więc oś Ox w punktach A = (− 2,0) i B = (4,0) . Szkicujemy tę sytuację.

PIC

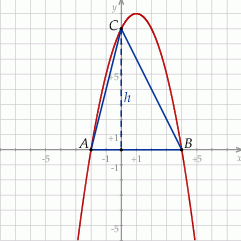
Liczymy pole trójkąta 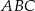ABC .

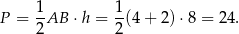
P = 1-AB ⋅ h = 1-(4+ 2)⋅8 = 24. 2 2

 
Odpowiedź: C

Wersja PDF