/Szkoła średnia/Zadania testowe/Funkcje - wykresy/Parabola/Dany wykres

Zadanie nr 2442728

Dodaj do ulubionych
Dodaj do rozwiązanych

Wzorem funkcji kwadratowej 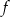f , której fragment wykresu przedstawiono na rysunku jest:

PIC

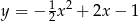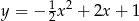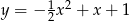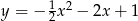
A) y = − 12x2 + 2x − 1 B) y = − 12x2 + 2x + 1 C) y = − 1x2 + x+ 1 2 D) 1 2 y = − 2x − 2x + 1

Rozwiązanie

Sposób I

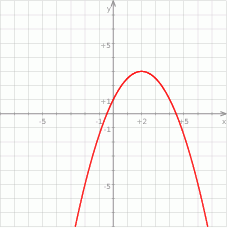
Wierzchołek paraboli z obrazka ma współrzędne 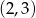(2,3) , więc musi to być parabola postaci

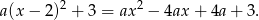
a(x − 2)2 + 3 = ax2 − 4ax + 4a + 3.

Ponieważ we wszystkich odpowiedziach współczynnik przy 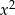x2 jest równy 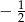− 1 2 , podstawiamy w powyższym wzorze a = − 1 2 .

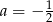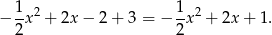
1- 2 1- 2 − 2 x + 2x − 2 + 3 = − 2 x + 2x + 1.

Sposób II

Z obrazka widać, że pierwsza współrzędna paraboli jest równa 2, więc ze wzoru na współrzędne wierzchołka musimy mieć

2 = −b--. 2a

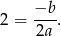
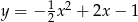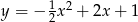Ten warunek spełniają funkcje 1 2 y = − 2 x + 2x− 1 i 1 2 y = − 2x + 2x + 1 . Aby ustalić, który z tych wzorów jest prawidłowy sprawdzamy, w którym dla 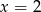x = 2 otrzymamy wartość 3.

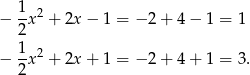
− 1x2 + 2x − 1 = −2 + 4 − 1 = 1 2 1-2 − 2x + 2x + 1 = −2 + 4 + 1 = 3.

 
Odpowiedź: B

Wersja PDF