Zadanie nr 5602001
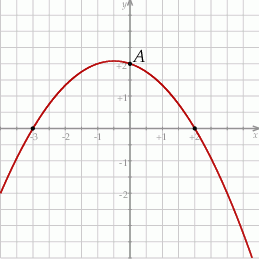
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 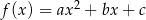 , której miejsca zerowe to:
, której miejsca zerowe to: 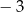 i 2. Do wykresu tego należy punkt
i 2. Do wykresu tego należy punkt 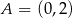 .
.
Współczynnik  we wzorze funkcji
we wzorze funkcji 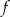 jest równy
jest równy
A) 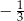 B)
B) 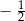 C)
C) 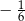 D)
D) 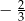
Rozwiązanie
Sposób I
Podane miejsca zerowe oznaczają, że mamy do czynienia z funkcją postaci
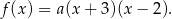
Wiemy ponadto, że
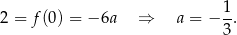
Sposób II
Z wykresu widać, że
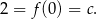
W takim razie funkcja ma wzór postaci 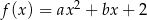 . Wiemy ponadto, że
. Wiemy ponadto, że
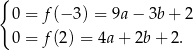
Aby obliczyć  dodajemy do pierwszego równania drugie pomnożone przez
dodajemy do pierwszego równania drugie pomnożone przez  .
.
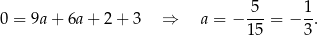
Odpowiedź: A

