Zadanie nr 7772964
Na rysunku obok jest przedstawiony fragment wykresu funkcji kwadratowej 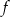 . Osią symetrii paraboli jest prosta o równaniu
. Osią symetrii paraboli jest prosta o równaniu 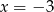 .
.
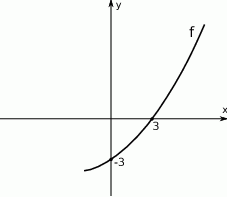
Rozwiązaniem nierówności 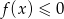 jest zbiór
jest zbiór
A) 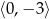 B)
B) 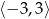 C)
C) 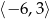 D)
D) 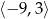
Rozwiązanie
Sposób I
Z wykresu widać, że jednym z miejsc zerowych danej funkcji kwadratowej jest 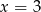 . Drugie miejsce zerowe łatwo wyznaczyć z podanej informacji o osi symetrii wykresu – punkt symetryczny do
. Drugie miejsce zerowe łatwo wyznaczyć z podanej informacji o osi symetrii wykresu – punkt symetryczny do 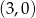 względem prostej
względem prostej 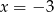 to punkt
to punkt 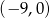 . Rozwiązujemy więc nierówność
. Rozwiązujemy więc nierówność
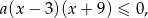
gdzie 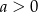 . Rozwiązaniem tej nierówności jest przedział
. Rozwiązaniem tej nierówności jest przedział 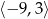 .
.
Sposób II
Podane równanie osi symetrii paraboli oznacza, że funkcja 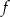 ma wzór postaci
ma wzór postaci
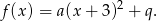
Wiemy ponadto, że 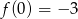 i
i 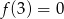 . Mamy zatem
. Mamy zatem
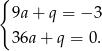
Odejmujemy od drugiego równania pierwsze i mamy 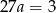 , czyli
, czyli 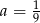 . Stąd
. Stąd
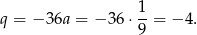
Rozwiązujemy teraz nierówność
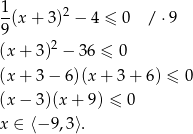
Odpowiedź: D

