/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Równanie prostej/Wzajemne położenie prostych

Zadanie nr 2157996

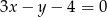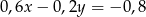Równania 3x − y − 4 = 0 oraz 0 ,6x − 0,2y = − 0,8 opisują proste w układzie współrzędnych, które
A) przecianją się pod kątem prostym
B) pokrywają się
C) są równoległe i nie pokrywają się
D) przecinają się pod innym kątem niż 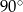∘ 90

Wersja PDF

Rozwiązanie

Pierwsze równanie możemy zapisać w postaci

y = 3x − 4

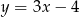
Przekształcamy drugie równanie

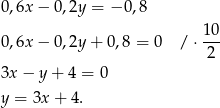
0,6x − 0,2y = − 0,8 10- 0,6x − 0,2y + 0 ,8 = 0 / ⋅ 2 3x − y + 4 = 0 y = 3x + 4 .

Współczynniki kierunkowe są sobie równe, ale wyrazy wolne są różne. Zatem proste są równoległe, ale się nie pokrywają.  
Odpowiedź: C

Wersja PDF