/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Równanie prostej/Wzajemne położenie prostych

Zadanie nr 4473071

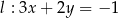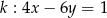
Proste o równaniach l : 3x + 2y = − 1 i k : 4x − 6y = 1
A) przecinają się w punkcie 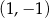(1,− 1) B) przecinają się w punkcie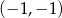 (− 1,− 1)
C) są równoległe D) są prostopadłe

Wersja PDF

Rozwiązanie

Zapiszmy proste w postaci kierunkowej

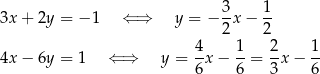
3 1 3x + 2y = −1 ⇐ ⇒ y = − --x − -- 2 2 4x − 6y = 1 ⇐ ⇒ y = 4x − 1-= 2x − 1- 6 6 3 6

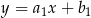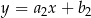Widać, że iloczyn współczynników kierunkowych jest równy -1, więc proste są prostopadłe (proste y = a1x + b1 i y = a2x+ b2 są prostopadłe jeżeli 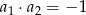a ⋅a = − 1 1 2 ). Jeszcze rysunek

PIC

 
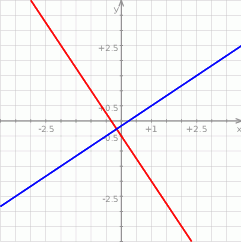
Odpowiedź: D

Wersja PDF