Zadanie nr 4957644
Proste o równaniach 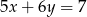 i
i 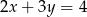 przecinają się w punkcie
przecinają się w punkcie 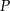 . Stąd wynika, że
. Stąd wynika, że
A) 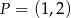 B)
B) 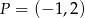 C)
C) 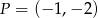 D)
D) 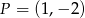
Rozwiązanie
Szukamy rozwiązania układu równań
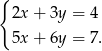
Dodajemy do drugiego równania pierwsze pomnożone przez 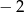 (żeby skrócić
(żeby skrócić 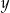 ).
).
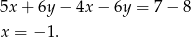
Zatem 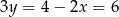 , czyli
, czyli 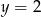 i
i 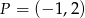
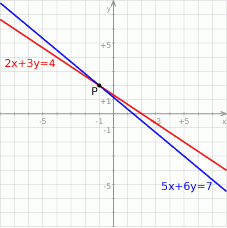
Odpowiedź: B

