Zadanie nr 6484452
Proste o równaniach 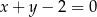 i
i 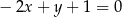 przecinają się w punkcie o współrzędnych
przecinają się w punkcie o współrzędnych
A) 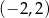 B)
B) 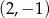 C)
C) 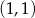 D)
D) 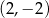
Rozwiązanie
Sposób I
Szukamy rozwiązania układu równań
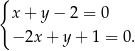
Odejmujemy od pierwszego równania drugie (żeby skrócić 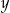 ).
).
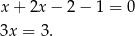
Zatem 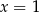 i
i 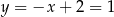 , czyli punkt wspólny to
, czyli punkt wspólny to 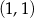 .
.
Sposób II
Rysujemy proste 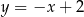 i
i 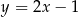 w układzie współrzędnych.
w układzie współrzędnych.
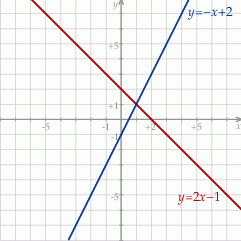
Z obrazka widać, że poprawna odpowiedź to 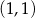 .
.
Odpowiedź: C

