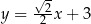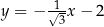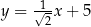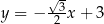Zadanie nr 6532323
W kartezjańskim układzie współrzędnych 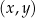 proste o równaniach:
proste o równaniach:
przecinają się w punktach, które są wierzchołkami czworokąta 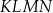 . Czworokąt
. Czworokąt 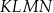 jest
jest
| A) | prostokątem, |
| B) | trapezem, który nie jest równoległobokiem |
| C) | równoległobokiem, który nie jest prostokątem, |
ponieważ
| 1) | czworokąt 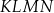 ma dwie osie symetrii. ma dwie osie symetrii. |
| 2) | dwie z tych prostych są prostopadłe. |
| 3) | dwie z tych prostych są równoległe. |
Rozwiązanie
Równanie trzeciej prostej możemy zapisać w postaci
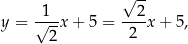
więc jest ona równoległa do pierwszej prostej. Ponadto
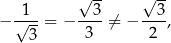
więc pozostałe dwie proste nie są równoległe.
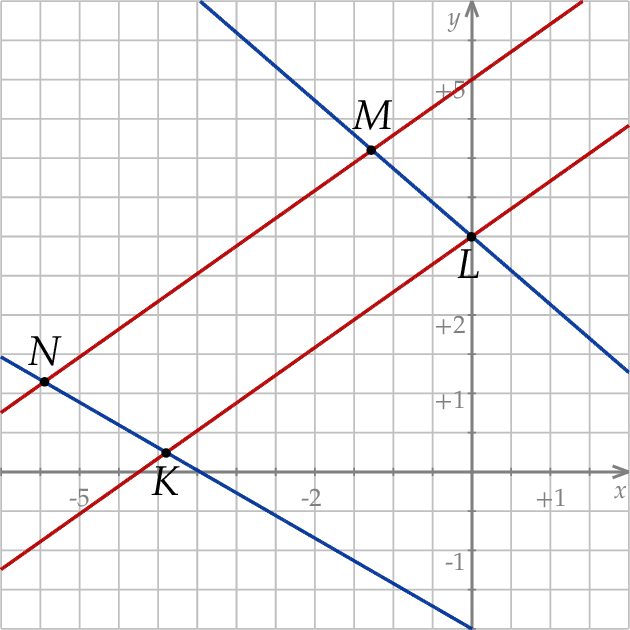
Czworokąt 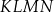 jest więc trapezem, ale nie jest równoległobokiem.
jest więc trapezem, ale nie jest równoległobokiem.
Odpowiedź: B, 3