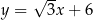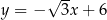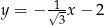Zadanie nr 9791193
W kartezjańskim układzie współrzędnych  proste o równaniach:
proste o równaniach:
przecinają się w punktach, które są wierzchołkami trójkąta 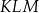 . Trójkąt
. Trójkąt 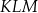 jest
jest
| A) równoramienny, | B) prostokątny, |
ponieważ
| 1) | oś 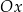 przechodzi przez jeden z wierzchołków tego trójkąta i środek jednego z boków tego trójkąta. przechodzi przez jeden z wierzchołków tego trójkąta i środek jednego z boków tego trójkąta. |
| 2) | dwie z tych prostych są prostopadłe. |
| 3) | oś 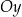 zawiera dwusieczną tego trójkąta. zawiera dwusieczną tego trójkąta. |
Rozwiązanie
Ponieważ
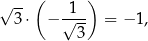
pierwsza i ostatnia prosta są prostopadłe. Trójkąt  jest więc prostokątny.
jest więc prostokątny.
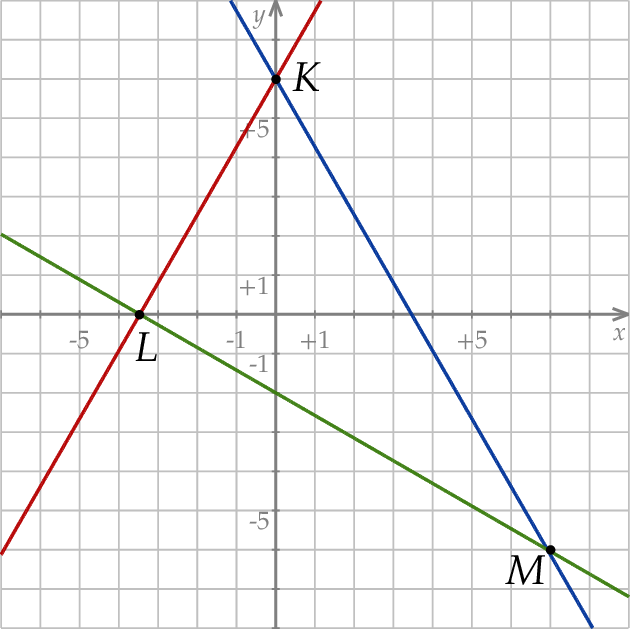
Odpowiedź: B, 2