Zadanie nr 2300290
Punkty 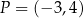 i
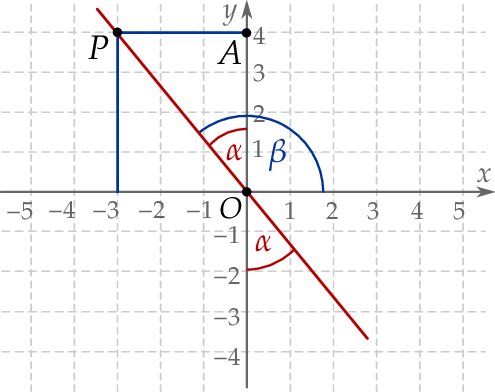
i 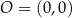 leżą na jednej prostej. Kąt
leżą na jednej prostej. Kąt  jest kątem jaki tworzy ta prosta z ujemną półosią
jest kątem jaki tworzy ta prosta z ujemną półosią 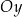 (zobacz rysunek).
(zobacz rysunek).
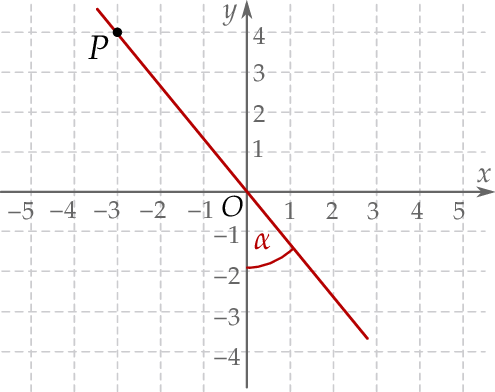
Wtedy tangens kąta  jest równy
jest równy
A) 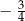 B)
B) 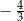 C)
C)  D)
D) 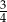
Rozwiązanie
Sposób I
Prosta przechodząca przez początek układu współrzędnych ma równanie postaci 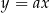 .
.
Współczynnik  wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 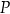 .
.
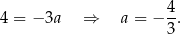
Obliczony współczynnik kierunkowy to dokładnie tangens kąta 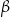 nachylenia prostej
nachylenia prostej 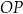 do osi
do osi 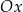 . Mamy zatem
. Mamy zatem
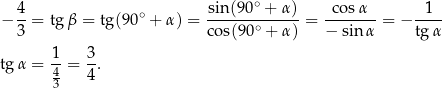
Sposób II
Tym razem patrzymy na trójkąt prostokątny 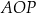 .
.
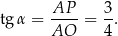
Odpowiedź: D

