Zadanie nr 4672776
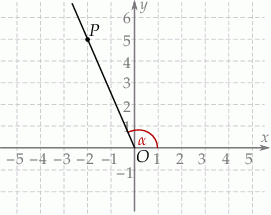
Tangens kąta  zaznaczonego na rysunku jest równy
zaznaczonego na rysunku jest równy
A) 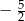 B)
B)  C)
C) 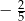 D)
D) 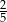
Rozwiązanie
Niech  będzie początkiem układu współrzędnych.
będzie początkiem układu współrzędnych.
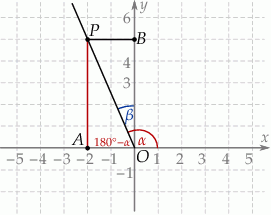
Sposób I
Zauważmy, że
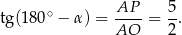
Stąd
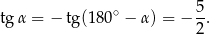
Sposób II
Tym razem popatrzmy na trójkąt 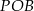 .
.
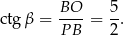
Stąd
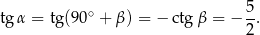
Sposób III
Napiszmy równanie prostej 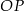 . Jest to prosta postaci
. Jest to prosta postaci 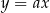 . Współczynnik
. Współczynnik  obliczamy podstawiając współrzędne punktu
obliczamy podstawiając współrzędne punktu 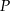 .
.
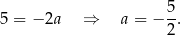
Otrzymany współczynnik kierunkowy to dokładnie interesujący nas 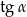 .
.
Sposób IV
Korzystamy z definicji funkcji trygonometrycznej 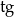 kąta skierowanego.
kąta skierowanego.
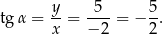
Odpowiedź: A

