Zadanie nr 6782408
Punkt 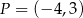 leży na końcowym ramieniu kąta
leży na końcowym ramieniu kąta  . Cosinus kąta
. Cosinus kąta  jest równy
jest równy
A)  B)
B) 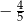 C)
C)  D)
D) 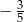
Rozwiązanie
Dorysujmy rzuty punktu 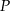 na osie okładu współrzędnych.
na osie okładu współrzędnych.
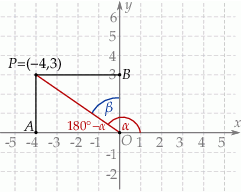
Sposób I
Korzystamy z definicji funkcji trygonometrycznych kąta skierowanego.
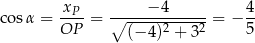
Sposób II
Zauważmy, że
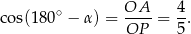
Stąd
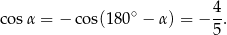
Sposób III
Tym razem popatrzmy na trójkąt 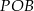 .
.
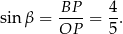
Stąd
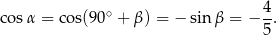
Sposób IV
Napiszmy równanie prostej 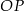 . Jest to prosta postaci
. Jest to prosta postaci 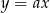 . Współczynnik
. Współczynnik  obliczamy podstawiając współrzędne punktu
obliczamy podstawiając współrzędne punktu 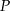 .
.
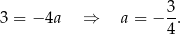
Otrzymany współczynnik kierunkowy to dokładnie 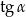 , więc
, więc
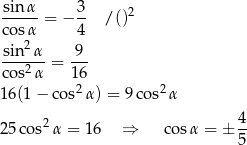
Ponieważ  jest kątem rozwartym, mamy stąd
jest kątem rozwartym, mamy stąd 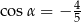 .
.
Odpowiedź: B

