Zadanie nr 8543709
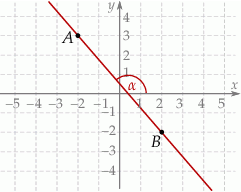
Tangens kąta  zaznaczonego na rysunku jest równy
zaznaczonego na rysunku jest równy
A)  B)
B) 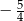 C)
C)  D)
D) 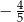
Rozwiązanie
Sposób I
Napiszmy równanie prostej przedstawionej na rysunku. Szukamy równania postaci 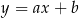 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 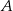 i
i 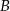 .
.
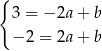
Odejmujemy od drugiego równania pierwsze (żeby skrócić 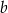 ) i mamy
) i mamy
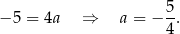
Ponieważ interesujący nas tangens to dokładnie współczynnik kierunkowy  prostej
prostej 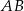 mamy
mamy
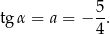
Sposób II
Tym razem patrzymy na trójkąt prostokątny 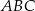 .
.
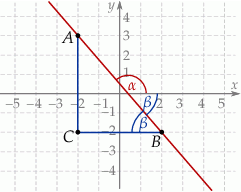
Mamy zatem
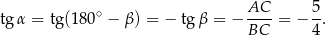
Odpowiedź: B

