Zadanie nr 8599594
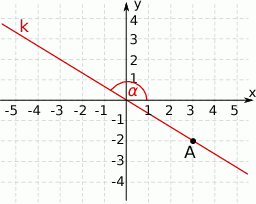
Na rysunku przedstawiona jest prosta 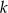 , przechodząca przez punkt
, przechodząca przez punkt 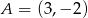 i przez początek układu współrzędnych, oraz zaznaczony jest kąt
i przez początek układu współrzędnych, oraz zaznaczony jest kąt  nachylenia tej prostej do osi
nachylenia tej prostej do osi 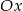 .
.
Zatem
A) 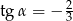 B)
B) 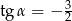 C)
C) 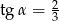 D)
D) 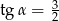
Rozwiązanie
Sposób I
Niech 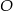 będzie początkiem układu współrzędnych, a
będzie początkiem układu współrzędnych, a 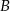 rzutem punktu
rzutem punktu 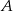 na oś
na oś 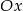 .
.
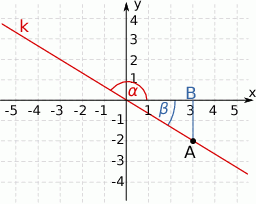
Mamy zatem
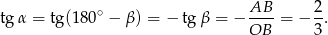
Sposób II
Napiszmy równanie prostej 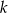 . Jest to prosta postaci
. Jest to prosta postaci 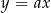 . Współczynnik
. Współczynnik  obliczamy podstawiając współrzędne punktu
obliczamy podstawiając współrzędne punktu 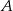 .
.
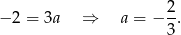
Otrzymany współczynnik kierunkowy to dokładnie interesujący nas 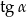 .
.
Odpowiedź: A

