/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Równanie prostej/Położenie względem osi

Zadanie nr 9898977

Wzór funkcji liniowej, której wykresem jest prosta nachylona do osi 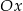Ox pod kątem o mierze 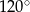120 ∘ i przechodzi przez punkt 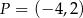P = (− 4,2) jest postaci
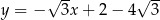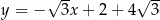
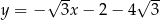A) y = − √ 3x + 2− 4√ 3- B) √ -- √ -- y = − 3x+ 2+ 4 3
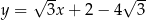
C) √ -- √ -- y = − 3x − 2 − 4 3 D) √ -- √ -- y = 3x + 2− 4 3

Wersja PDF

Rozwiązanie

Szkicujemy prostą w układzie

PIC

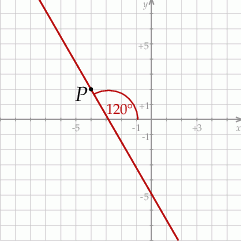
Podany kąt nachylenia prostej 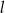l oznacza, że jej współczynnik kierunkowy jest równy

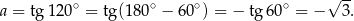
√ -- a = tg120 ∘ = tg(180∘ − 60∘) = − tg60 ∘ = − 3.

To oznacza, że prosta 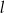l ma równanie postaci

√ -- y = − 3x + b.

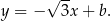
Współczynnik 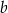b wyznaczamy podstawiając współrzędne punktu (− 4,2) .

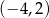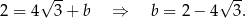
2 = 4 √ 3+ b ⇒ b = 2 − 4√ 3.

Szukana prosta ma więc równanie

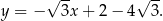
-- -- y = − √ 3x + 2 − 4√ 3 .

 
Odpowiedź: A

Wersja PDF