Zadanie nr 3934268
Dane są punkty 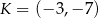 oraz
oraz 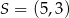 . Punkt
. Punkt 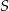 jest środkiem odcinka
jest środkiem odcinka 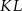 . Wtedy punkt
. Wtedy punkt 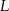 ma współrzędne
ma współrzędne
A) 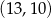 B)
B) 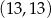 C)
C) 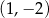 D)
D) 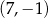
Rozwiązanie
Sposób I
Wiemy, że 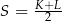 , więc
, więc
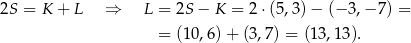
Sposób II
Ze wzoru:
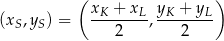
na współrzędne środka 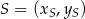 odcinka o końcach
odcinka o końcach 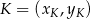 i
i 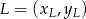 mamy
mamy
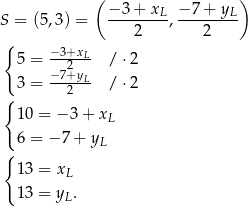
Zatem 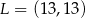 .
.
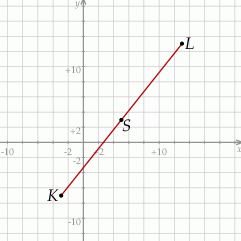
Odpowiedź: B

