Zadanie nr 5735614
Przez punkt 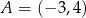 poprowadzono prostą
poprowadzono prostą 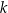 , która przecina proste
, która przecina proste 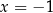 i
i 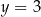 w takich punktach
w takich punktach 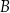 i
i 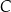 , że
, że 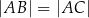 . Długość odcinka
. Długość odcinka 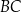 jest równa
jest równa
A) 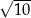 B)
B) 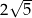 C)
C) 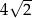 D)
D) 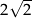
Rozwiązanie
Szkicujemy opisaną sytuację.
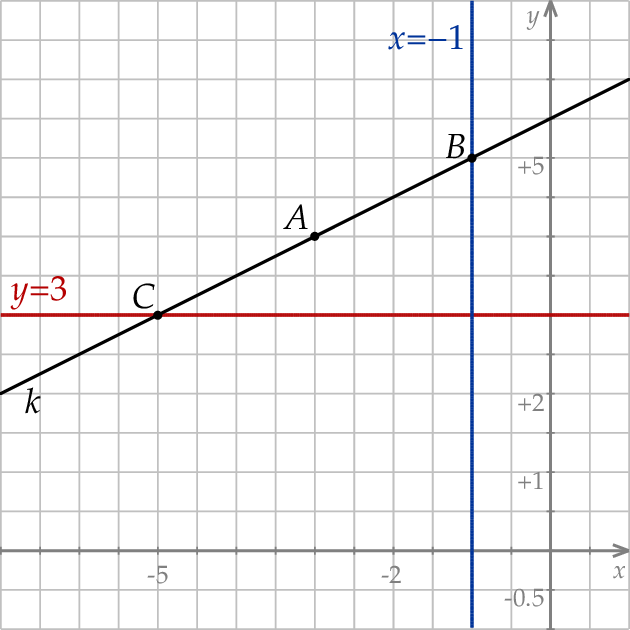
Wiemy, że punkt 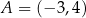 jest środkiem odcinka
jest środkiem odcinka 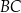 ,
, 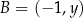 i
i 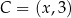 . Mamy zatem
. Mamy zatem
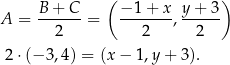
Stąd 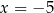 i
i 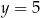 , czyli
, czyli 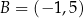 i
i 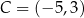 . Zatem
. Zatem
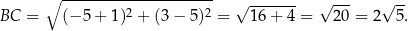
Odpowiedź: B

