/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Czworokąt/Kwadrat/Różne

Zadanie nr 3003045

Dodaj do ulubionych
Dodaj do rozwiązanych

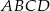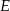W kwadracie ABCD punkt E jest środkiem boku 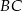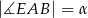BC , |∡EAB | = α . Wynika stąd, że
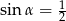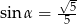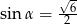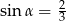
A) sin α = 1 2 B) √ - sinα = --5 5 C) √ 6 sin α = -2- D) 2 sinα = 3

Rozwiązanie

Zaczynamy od rysunku

PIC

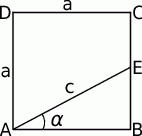
Z twierdzenia Pitagorasa wyznaczamy długość odcinka 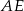AE

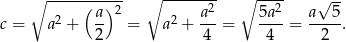
∘ -----(--)-- ∘ -------- ∘ ---- √ -- 2 a- 2 2 a2- 5a2- a--5- c = a + 2 = a + 4 = 4 = 2 .

Teraz już łatwo rozwiązać zadanie

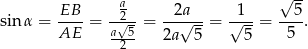
√ -- EB-- -a2-- --2a-- -1-- --5- sinα = AE = a√5-= √ --= √ --= 5 . 2 2a 5 5

 
Odpowiedź: B

Wersja PDF