Zadanie nr 2372767
Trójkąt 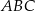 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 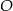 . Jeśli
. Jeśli 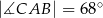 i
i 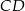 jest średnicą okręgu, to miara kąta
jest średnicą okręgu, to miara kąta 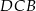 jest równa
jest równa
A) 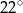 B)
B) 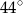 C)
C) 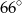 D)
D) 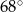
Rozwiązanie
Szkicujemy opisaną sytuację.
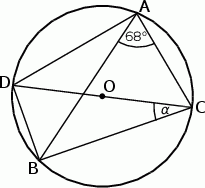
Kąty 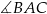 i
i 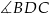 są oparte na tym samym łuku, więc
są oparte na tym samym łuku, więc
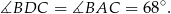
Odcinek  jest średnicą okręgu, więc trójkąt
jest średnicą okręgu, więc trójkąt  jest prostokątny. Stąd
jest prostokątny. Stąd
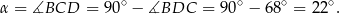
Odpowiedź: A

