Zadanie nr 2848406
Na okręgu o środku w punkcie 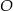 leżą punkty
leżą punkty 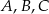 (zobacz rysunek).
(zobacz rysunek).
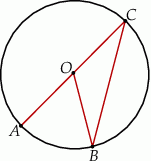
Odcinek 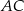 jest średnicą okręgu. Kąt
jest średnicą okręgu. Kąt 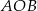 ma miarę
ma miarę 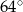 . Kąt
. Kąt 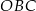 ma miarę równą
ma miarę równą
A) 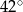 B)
B) 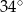 C)
C) 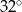 D)
D) 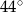
Rozwiązanie
Sposób I
Zauważmy, że trójkąt 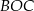 jest równoramienny, więc
jest równoramienny, więc
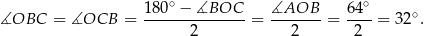
Sposób II
Korzystając z twierdzenia o kątach wpisanym i środkowym, mamy
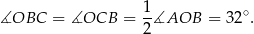
Odpowiedź: C

