/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Trójkąt/Równoboczny/Pole

Zadanie nr 4172941

Dodaj do ulubionych
Dodaj do rozwiązanych

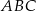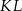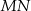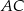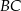W trójkącie równobocznym ABC poprowadzono odcinki KL i MN , które podzieliły boki AC i BC na trzy równe części. Stosunek pola trójkąta 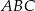ABC do pola trapezu 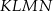KLMN jest równy

PIC

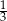A) 3 B) 13 C) 9 D) 6

Rozwiązanie

Sposób I

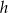Jeżeli oznaczymy przez a długość boku trójkąta, a przez h długość jego wysokości, to wysokość trapezu jest równa 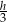h3 oraz

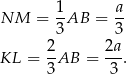
NM = 1AB = a- 3 3 2- 2a- KL = 3AB = 3 .

Zatem

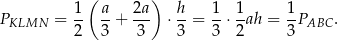
( ) 1- a- 2a- h- 1- 1- 1- PKLMN = 2 3 + 3 ⋅3 = 3 ⋅2 ah = 3 PABC .

Zatem

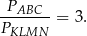
-PABC-- P = 3 . KLMN

Sposób II

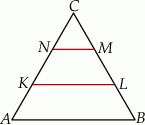
Dorysowując odcinki równoległe do boków łatwo podzielić trójkąt równoboczny na 9 przystających trójkątów równobocznych.

PIC

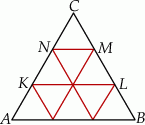
Widać teraz, że interesujący nas stosunek pól jest równy

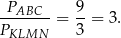
-PABC--= 9-= 3. PKLMN 3

 
Odpowiedź: A

Wersja PDF