Zadanie nr 3358431
Dany jest trójkąt prostokątny 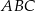 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 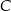 . Jeśli
. Jeśli 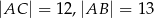 , to tangens najmniejszego kąta w tym trójkącie jest równy
, to tangens najmniejszego kąta w tym trójkącie jest równy
A) 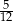 B)
B) 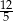 C)
C) 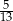 D)
D) 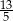
Rozwiązanie
Ponieważ przy wierzchołku 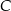 leży kąt prosty, więc przyprostokątnymi będą
leży kąt prosty, więc przyprostokątnymi będą 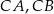 . Zatem
. Zatem 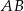 jest przeciwprostokątną. Obliczamy z twierdzenia Pitagorasa długość trzeciego boku trójkąta
jest przeciwprostokątną. Obliczamy z twierdzenia Pitagorasa długość trzeciego boku trójkąta
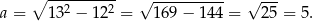
Wykonujemy rysunek pamiętając, że najmniejszy kąt jest zawsze naprzeciwko najkrótszego boku
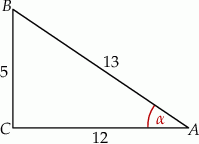
Teraz już łatwo obliczyć interesujący nas tangens
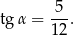
Odpowiedź: A

