Zadanie nr 1917319
Trójkąt prostokątny o przyprostokątnych długości 8 i 6 obrócono wokół dłuższej przyprostokątnej. Pole powierzchni bocznej tak otrzymanej bryły jest równe
A) 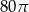 B)
B) 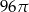 C)
C) 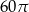 D)
D) 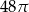
Rozwiązanie
Zaczynamy od rysunku
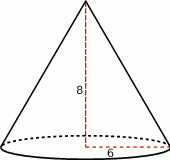
Zanim obliczymy pole powierzchni bocznej, wyznaczmy najpierw długość tworzącej. Robimy to z twierdzenia Pitagorasa
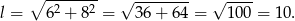
Zatem pole powierzchni bocznej wynosi
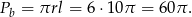
Odpowiedź: C

