Zadanie nr 9775494
Dany jest trójkąt prostokątny o długościach boków 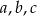 , gdzie
, gdzie 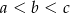 . Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt
. Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt 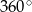 , otrzymujemy bryłę, której pole powierzchni całkowitej jest równe
, otrzymujemy bryłę, której pole powierzchni całkowitej jest równe
A) 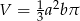 B)
B) 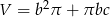 C)
C) 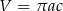 D)
D) 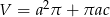
Rozwiązanie
W wyniku opisanej operacji otrzymujemy oczywiście stożek.
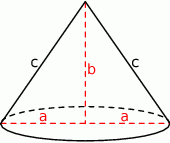
Pole powierzchni całkowitej tego stożka jest równe
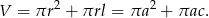
Odpowiedź: D

