/Szkoła średnia/Zadania testowe/Kombinatoryka/Zbiory liczb/Cyfry

Zadanie nr 5796596

Wszystkich liczb naturalnych pięciocyfrowych, w których cyfrą jedności jest 4, cyfra setek jest liczba nieparzystą, a cyfra tysięcy jest liczbą podzielną przez 3 jest
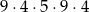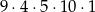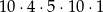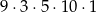
A) 9 ⋅4⋅ 5⋅9 ⋅4 B) 9 ⋅4 ⋅5⋅ 10⋅1 C) 10 ⋅4 ⋅5⋅1 0⋅1 D) 9 ⋅3⋅ 5⋅10 ⋅1

Wersja PDF

Rozwiązanie

Wybieramy kolejne cyfry liczby pięciocyfrowej tak, aby były spełnione warunki zdania. Cyfrę dziesiątek tysięcy możemy wybrać na 9 sposobów (nie może być zerem), cyfrę tysięcy na 4 sposoby (może być 0, 3, 6 lub 9), cyfrę setek na 5 sposobów, cyfrę dziesiątek na 10 sposobów i wreszcie cyfrę jedności na 1 sposób (musi być 4). W sumie jest więc

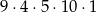
9 ⋅4 ⋅5⋅ 10⋅1

takich liczb.  
Odpowiedź: B

Wersja PDF