Zadanie nr 6011968

Wszystkich liczb pięciocyfrowych jest

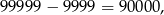
ale nas interesują tylko liczby, w których iloczyn cyfr jest niezerowy – takich liczb jest

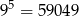
(każdą cyfrę możemy wybrać na 9 sposobów).

Zamiast liczyć ile jest liczb spełniających warunki zadania, obliczmy ile jest liczb, które tych warunków nie spełniają.

Musimy odrzucić 11111 oraz liczby, w których iloczyn cyfr jest liczbą pierwszą. W takich liczbach jedna cyfra musi być jedną z cyfr: 2,3,5,7, a pozostałe muszą być równe 1. Jest więc

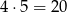
takich liczb (na 4 sposoby wybieramy cyfrę różną od 1 i na 5 sposobów miejsce umieszczenia tej liczby).

To oznacza, że liczb spełniających warunki zadania jest

 
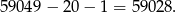
Odpowiedź: B