Zadanie nr 7836365
Ile jest liczb naturalnych sześciocyfrowych, których iloczyn cyfr jest różny od 49?
A) 899 970 B) 899 969 C) 899 985 D) 899 984
Rozwiązanie
Zastanówmy się najpierw, kiedy iloczyn cyfr w liczbie sześciocyfrowej może być równy 49? Aby tak było, dwie z cyfr tej liczby muszą być równe 7, a cztery pozostałe muszą być równe 1. Jest więc
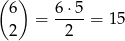
takich liczb (wybieramy miejsca dla siódemek, a na pozostałych miejscach umieszczamy jedynki).
Wszystkich liczb sześciocyfrowych jest
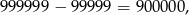
więc liczb spełniających warunki zadania jest
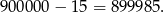
Odpowiedź: C

