Zadanie nr 9898456
Liczba wszystkich dodatnich liczb pięciocyfrowych, które są podzielne przez 3, i których cyfry należą do zbioru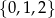 
, jest równa
A) 81 B) 54 C) 162 D) 243
Rozwiązanie
Pierwszą cyfrę 
liczby opisanej w treści zadania możemy wybrać na 2 sposoby (nie może być zerem), potem każdą z kolejnych 3 cyfr 
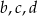wybieramy na 3 sposoby.
Zastanówmy się teraz nad ostatnią cyfrą 
– musimy ją dobrać tak, aby suma
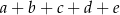
dzieliła się przez 3. To oznacza, że przy wyborze 
nie mamy żadnego wyboru: wybieramy 0, gdy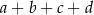 
dzieli się przez 3, wybieramy 2 jeżeli 
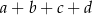daje resztę 1 przy dzieleniu przez 3, i wreszcie wybieramy 1 jeżeli 
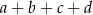daje resztę 2 przy dzieleniu przez 3.
W sumie są więc
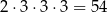
takie liczby.
Odpowiedź: B
