Zadanie nr 9822217
Przekątna przekroju osiowego walca jest o 13 dłuższa od promienia podstawy tego walca, oraz o 2 dłuższa od jego wysokości. Pole podstawy tego walca jest równe
A) 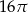 B)
B) 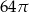 C)
C) 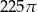 D)
D) 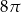
Rozwiązanie
Oznaczmy przez  promień podstawy walca.
promień podstawy walca.
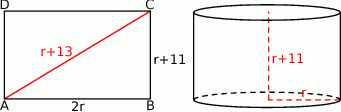
Piszemy twierdzenie Pitagorasa w trójkącie 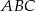 .
.
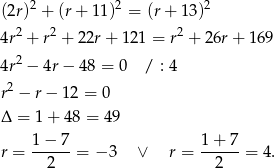
Ujemne rozwiązanie odrzucamy i mamy 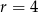 . Pole podstawy jest więc równe
. Pole podstawy jest więc równe
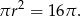
Odpowiedź: A

