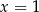/Szkoła podstawowa/Funkcje

Zadanie nr 1595158

Dodaj do ulubionych
Dodaj do rozwiązanych

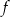Funkcja f każdej liczbie naturalnej przypisuje liczbę jej cyfr w układzie dziesiętnym.

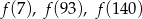  • Oblicz f(7), f(93), f(14 0) .
  • Dla ilu różnych argumentów funkcja 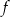f przyjmuje wartość 2?
  • Dla ilu różnych argumentów funkcja f przyjmuje wartość 3?
  • Rozwiąż równanie f (x) = x .

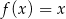Rozwiązanie

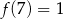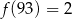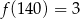  • Liczby 7, 93, 140 składają się odpowiednio z 1, 2 i 3 cyfr, więc f(7) = 1 , f(93) = 2 i f(140) = 3 .  
    Odpowiedź: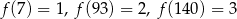 f(7) = 1, f (93) = 2, f(140) = 3
  • Funkcja f przyjmuje wartość 2 dla liczb, które składają się z dwóch cyfr. Dwucyfrowe liczby naturalne to:
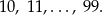
    10 , 11,..., 99.

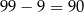    Jest ich 99 − 9 = 90 .  
    Odpowiedź: 90

  • Funkcja 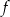f przyjmuje wartość 3 dla liczb, które składają się z trzech cyfr. Trzycyfrowe liczby naturalne to: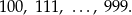
    10 0, 11 1, ..., 999.

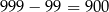    Jest ich 999 − 9 9 = 900 .  
    Odpowiedź: 900

  • Jeżeli liczba ma więcej niż dwie cyfry, to na pewno jest większa niż liczba jej cyfr. Jeżeli natomiast liczba jest jednocyfrowa, to warunek 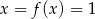x = f (x) = 1 oznacza, że x = 1 .  
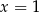    Odpowiedź: x = 1
Wersja PDF